二进制

二进制与其他进制的换算

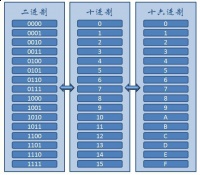
二进制 是计算技术中广泛采用的一种数制。二进制数是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”。二进制数也是采用位置计数法，其位权是以2为底的幂。

二进制是世界上第一台计算机上用的算法，最古老的计算机里有一个个灯泡，当运算的时候，比如要表达“一”，第一个灯泡会亮起来。要表达“二”，则第一个灯泡熄灭，第二个灯泡就会亮起来。

二进制历史

关于二进位制记数法，在17世纪已经萌芽，17世纪后半叶，莱布尼茨结合中国的阴阳学说进一步完善了进位制，在十进位制中，他形象地用１表示上帝，用０表示虚无，上帝从虚无中创造出所有的实物，恰好在数学中用１和０表示了所有的数。从理论上分析，在所有可能的进位制的基底中最小的基底是二进位制的基底。在二进位制中，只有数码１和０，其他任何数都用一行0、１表示，加法表和乘法表仅由１＋０和１×０，其他任何数都用一行０、１表示，加法表和乘法表仅由１＋０和１×０组成。

二进制与其他进制的转换

二进制数转换成十进制数

由二进制数转换成十进制数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。这种做法称为"按权相加"法。

• 二进制转十进制
  方法："按权展开求和"

例：

（1011.01）2 ＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10
＝（8＋0＋2＋1＋0＋0.25）10
＝（11.25）10

十进制转二进制

十进制整数转二进制数："除以2取余，逆序输出"

例：（89）10＝（1011001）2

2 89
2 44 …… 1
2 22 …… 0
2 11 …… 0
2 5 …… 1
2 2 …… 1
2 1 …… 0
0 …… 1 

八进制转二进制

例：将八进制的37.416转换成二进制数：

37 ． 4 1 6
011 111 ．100 001 110
（37.416）8 ＝（11111.10000111）2

例：将二进制的10110.0011 转换成八进制：

0 1 0 1 1 0 . 0 0 1 1 0 0(每三位对应一个八进制数)
2 6 . 1 4
即：（10110.011）2 ＝（26.14）8 

十六进制转二进制

例：将十六进制数5DF.9 转换成二进制：

5 D F ． 9
0101 1101 1111．1001
（5DF.9）16 ＝（10111011111.1001）2

例：将二进制数1100001.111 转换成十六进制：

0110 0001 ． 1110(每四位对应一个十六进制数)
6 1 ． E
（1100001.111）2 ＝（61.E）16

相关条目

• 八进制
• 十进制
• 十六进制

参考来源

• 参考来源1
• 参考来源2